In this article, we’ll discover how much swap fees asymmetric LPs generate when compared to symmetric ones. This is important when calculating incentive rewards for such pools.
For example, a 80%ETH-20%USDC LP earns less than a 50%ETH-50%USDC LP of the same value. And a 95%ETH-5%USDC LP generates even less. But how much less?

This is part 2 of Tsundoku’s journey to make the perfect yield farm. Read the intro article first.
Tsundoku Finance is building custom farms for Balancer’s AMM model. Tsundoku will incentivize individual tokens instead of hardcoded pools, so liquidity providers can create pools of any composition and get incentive rewards for it.
TL;DR — in the worst case, LP’s income from swap fees goes down quadratically with more asymmetry in the pool. We proved this both numerically and analytically.
The formula for how much fees an LP generates when compared to symmetric LP is:
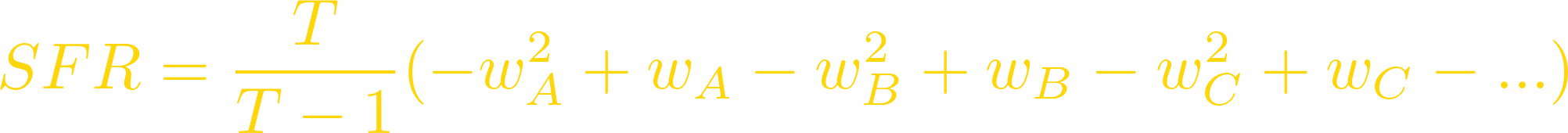
wᵢ are token weights; T is the amount of different tokens in the LP
Asymmetric pools in Weighted Constant Product AMMs greatly lower impermanent losses for liquidity providers. You can have great exposure to your favorite token while also providing liquidity for it.
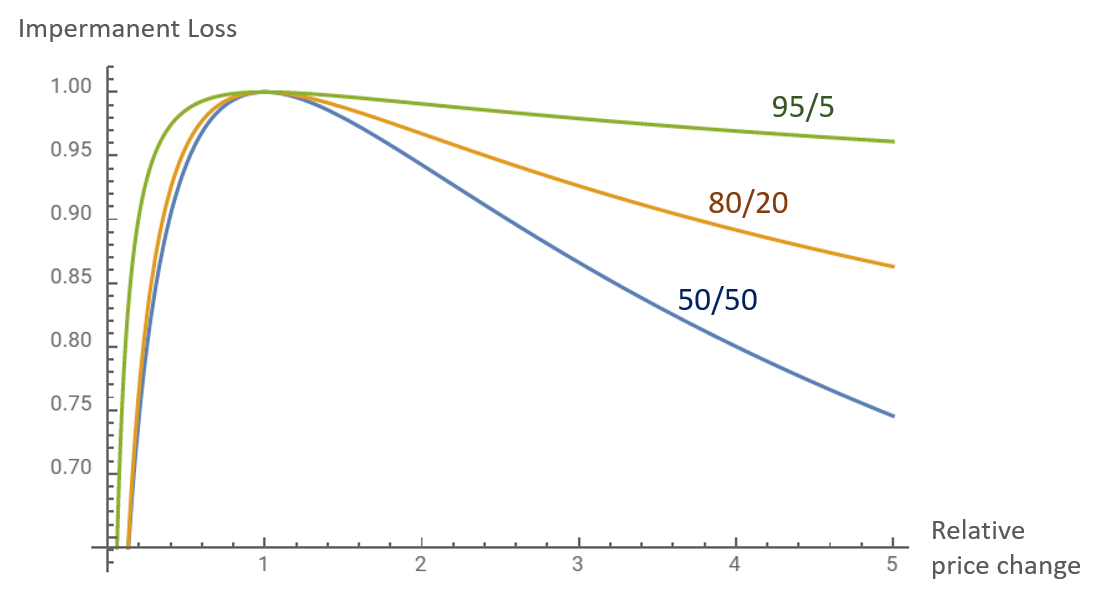
But this comes at a cost. Asymmetric pools have higher slippage, which makes possible arbitrage (the main source of swap fees) much smaller.
Let’s see some examples. In these, no new LP deposits or withdraws are made.
Also consider 1 ETH costs 1 USDC for simplicity’s sake.
Note: you can find the formula to calculate pools’ balances after price changes in the last chapter of the article.
Example 1
- A symmetric pool is a 50%/50% LP, consisting of 1000 ETH and 1000 USDC.
- ETH pumps 2x, and now costs 2 USDC.
- The pool’s new balance will be 707.1 ETH and 1414.2 USDC.
- The balance changed thanks to an arbitrageur, who fixed the price in the pool and made profit from it. He sold 414.2 USDC to buy cheap ETH.
- So, while ETH was pumping, at least 414.2 USDC was swapped within the pool.
- If the pool has a swapping fee, then the earnings are: (414.2 * swap_fee) USDC
Now let’s look at the behaviour of an asymmetric pool of the same value.
(Also starts from 1 ETH costing 1 USDC)
- The asymmetric pool is a 80%/20% LP, consisting of 1600 ETH and 400 USDC.
- ETH pumps 2x, and now costs 2 USDC.
- The pool’s new balance will be 1392.88 ETH and 696.44 USDC.
- The arbitrageur swapped 296.44 USDC in the pool.
- So the earnings are: (296.44 * swap_fee) USDC
296.44 / 414.2 ≈ 0.71 — Let’s call this “Swap Fee Ratio”
1 - 0.71 = 0.29 — Let’s call this “Swap Fee Loss”
The 80%/20% asymmetric pool generates ~29% less swap fees when the 80% token pumps 2x.
Example 2
Let’s try the same pools but a 2x dump instead of a 2x pump.
- A symmetric pool is a 50%/50% LP, consisting of 1000 ETH and 1000 USDC.
- ETH dumps 2x, and now costs 0.5 USDC.
- The pool’s new balance will be 1414.2 ETH and 707.1 USDC.
- Now the arbitrageur sold 414.2 ETH to the pool.
- The earnings are: (414.2 * swap_fee) ETH
And the asymmetric one:
- The asymmetric pool is a 80%/20% LP, consisting of 1600 ETH and 400 USDC.
- ETH dumps 2x, and now costs 0.5 USDC.
- The pool’s new balance will be 1837.9 ETH and 229.74 USDC.
- The arbitrageur sold 237.9 ETH to the pool.
- The earnings are: (237.9 * swap_fee) ETH
237.9 / 414.2 ≈ 0.57
The Swap Fee Ratio is even smaller in this case. So the 80%/20% asymmetric pool earns ~43% less when the 80% token dumps 2x.
These values (0.71 and 0.57) are the ratio of swap fees of an asymmetric LP to swap fees of a symmetric LP. We call it the Swap Fee Ratio (SFR).
Higher SFR = more fees generated by LP.
Great, we calculated how much the 80%/20% pool earns compared to the 50%/50% one when the price of either tokens changes 2x.
Let’s calculate SFR for the 2x pump/dump, but for more asymmetric types of pools: 99%/1%, 90%/10%, 5%/95%, and everything in between.
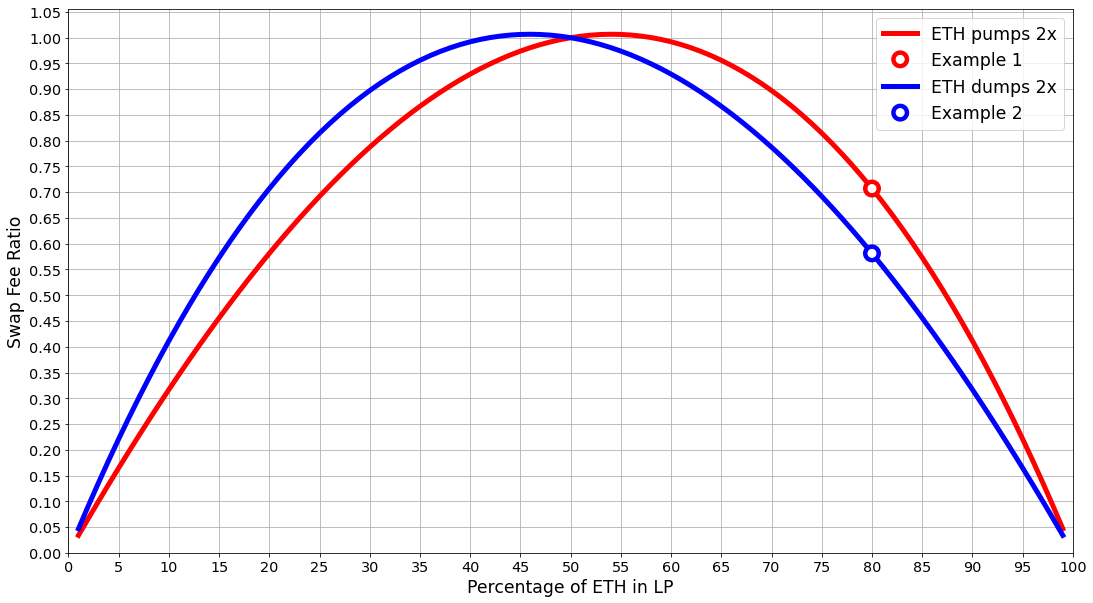
SFR equals to 1 in 50%/50% LPs, which is the symmetric LP scenario.
In general, SFR becomes smaller with more asymmetry. This means that the LP earns less swap fees.
Although, slightly asymmetric positions sometimes earn more, with SFR above 1. For example, this is seen on the plot for the 55%/45% case when ETH pumps 2x.
Let’s calculate more examples for different price changes.
(If the above animation doesn’t autoplay, right click it, then choose “Show All Controls”, then unpause it. No idea why this happens sometimes.)
On this animation, whichever line is higher, generates more fees. So, an LP with a bigger ETH weight always performs better when ETH pumps rather than when ETH dumps.
On small price changes, these lines start looking really similar to a parabola. We can use it as an index of how performant an LP is.
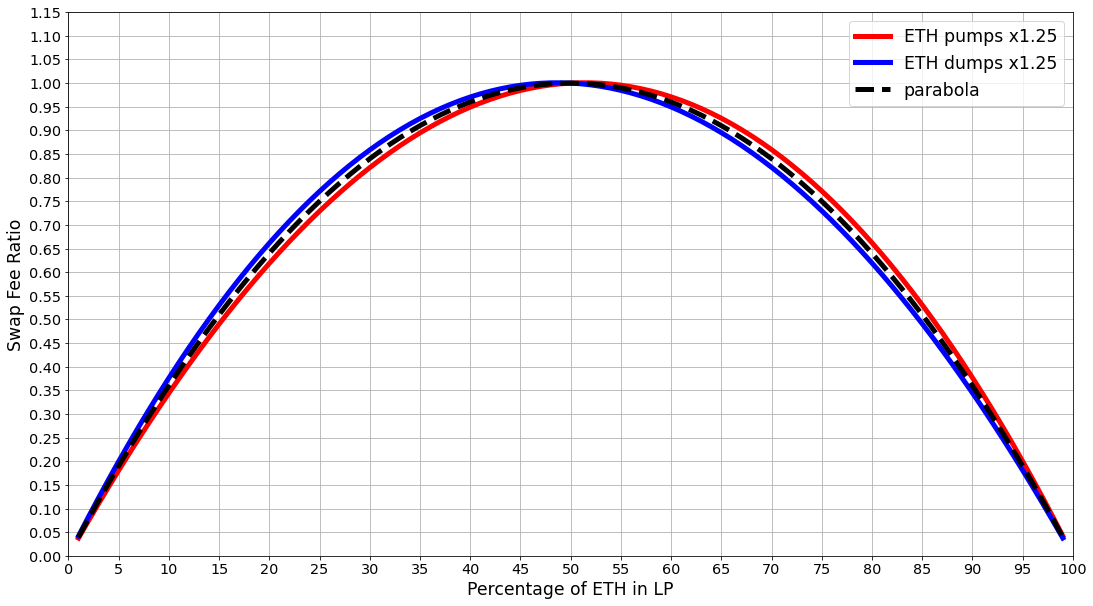
So, on pumps and dumps an asymmetric LP performs differently. But how does it perform on average? Let’s take the average of an LP’s performance. We will just sum up the red and blue charts, then divide by 2.
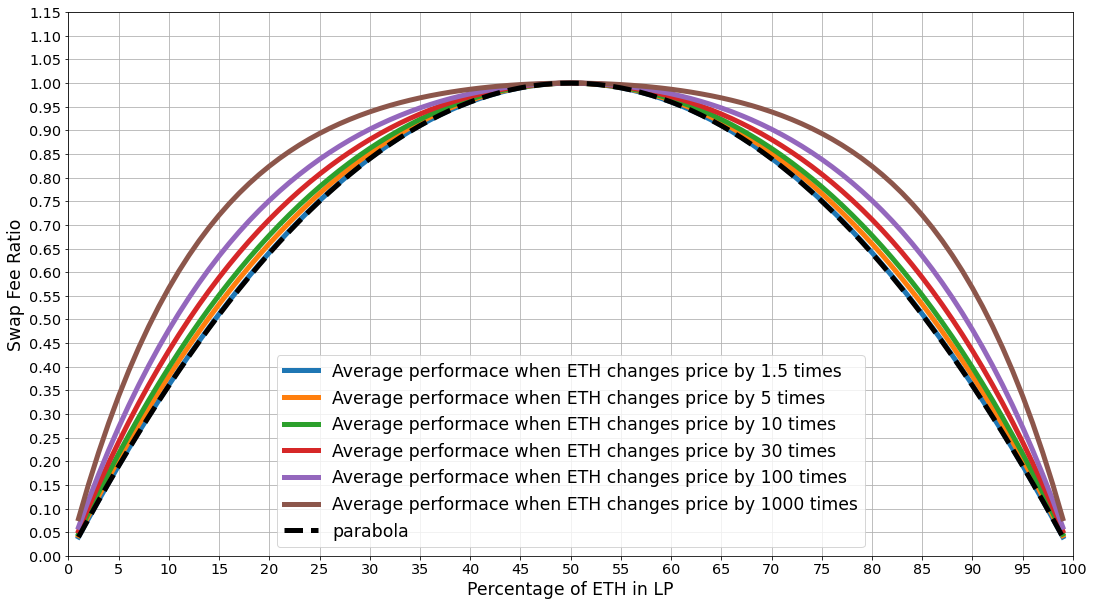
This plot shows that the average performance of any asymmetric LP never goes below the parabola. So, the underperformances in some cases are always cancelled out by the LP’s overperformances over the parabola.
On average, asymmetric LPs generate at least as much fees as the parabola.
And on very small price changes, like ±1%, it performs almost identically to the parabola. The smaller the change, the closer to the parabola.
So, a double-token LP with weights a and b, generates at least (-4_a^2 + 4a) as much fees as a double-token LP with weights _0.5 and 0.5.
So, a 80%/20% LP’s average SFR is (-40.8^2 + 40.8) = 0.64. This means that it generally generates 36% less swap fees as a 50%/50% LP.
What about LPs with multiple tokens?
The generalized formula for Swap Fee Ratio for a multiple-token pool is:
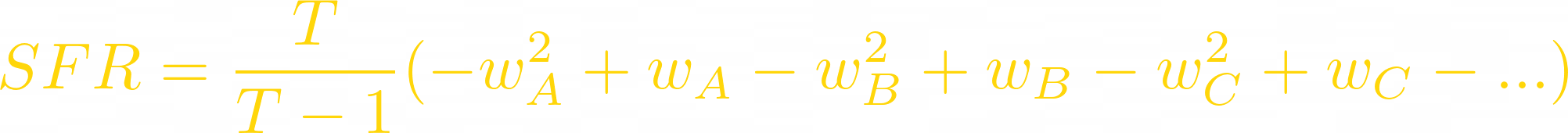
Where wᵢ are token weights, and T is the amount of different tokens in the LP.
You can find the proof for this formula after the conclusion (because the math is quite expansive and some people may want to skip it).
Conclusion
In normal day-to-day market (±1% daily volatility on tokens), LP’s swap fee revenue goes down quadratically when any of its token’s weight diverges from symmetry.
SFR is a formula for the minimal possible swap fee revenue of an LP in a normal day-to-day market. When compared to symmetric LP, asymmetric LP will always earn at least as much as the formula tells us.
The swap fees can only be bigger than that, because of higher volatility and retail traders.
We will be using this formula for incentives calculations for Tsundoku Finance which we’ll discuss in next articles. Stay tuned and follow us on social media and stuff. (Twitter, Telegram)
Formal proof that on smaller price changes, an asymmetric LP’s swap fee performance converges to a parabola.
This is how Uniswap’s Constant Product formula looks: x * y = k
Balancer’s Constant Product formula is not much different, except it can have more variables, and variables can have weights:
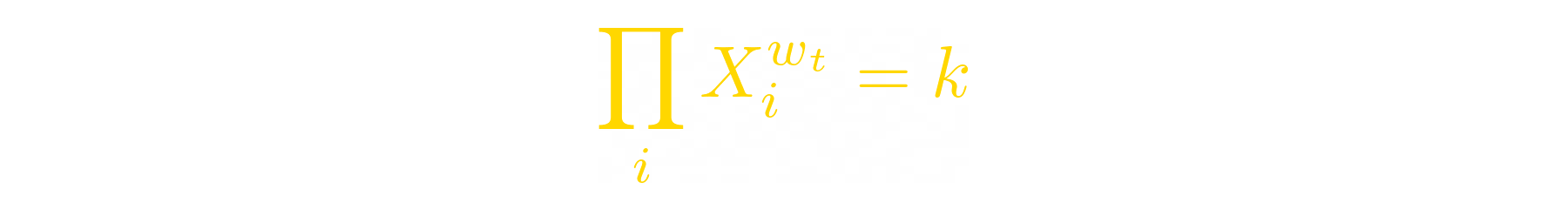
Where i = A,B,C… — these are different tokens in the pool (e.g. ETH, USDC, BTC…);
Xᵢ is the amount of token i in the pool;
wᵢ is weight of token i in the pool (w₁ + w₂ + w₃ + … = 1);
k is invariant.
To express the price a A through B, we use this formula:
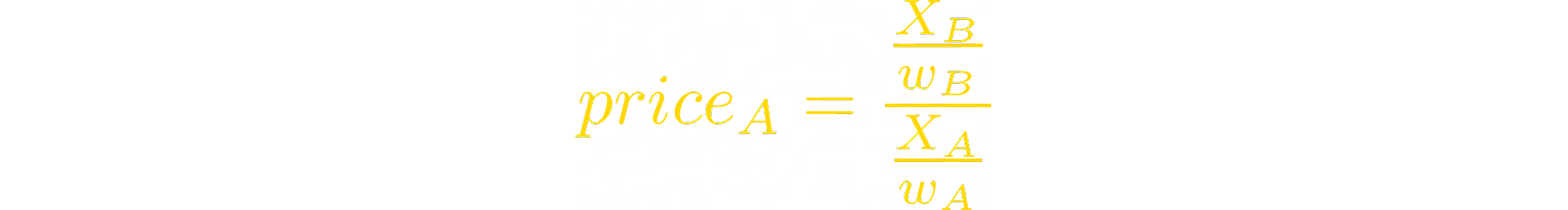
When price of A increases n times, the balances of tokens change:
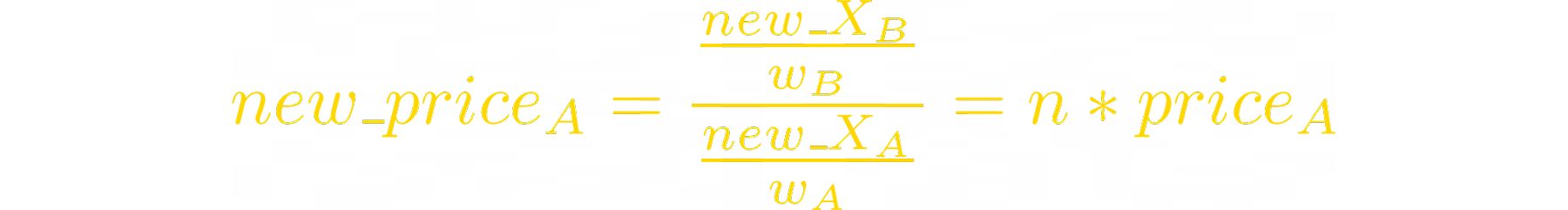
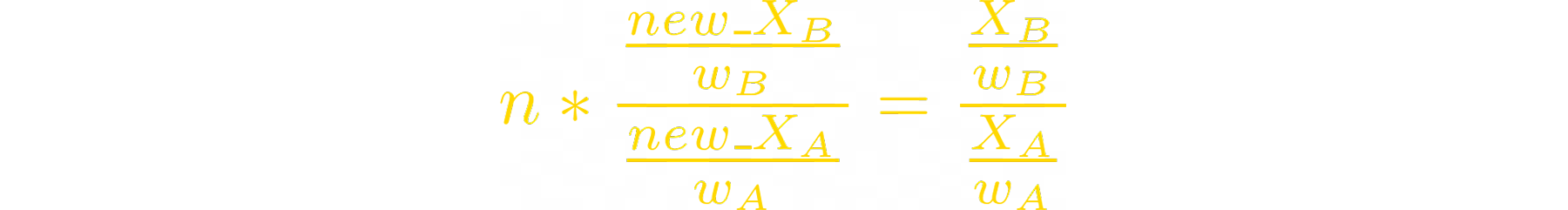
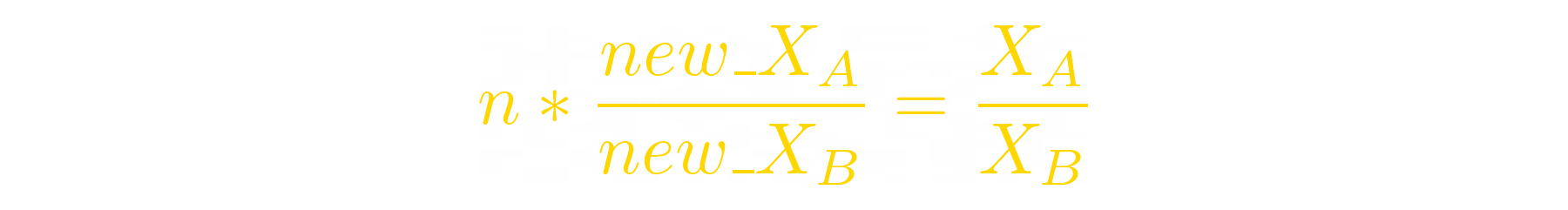
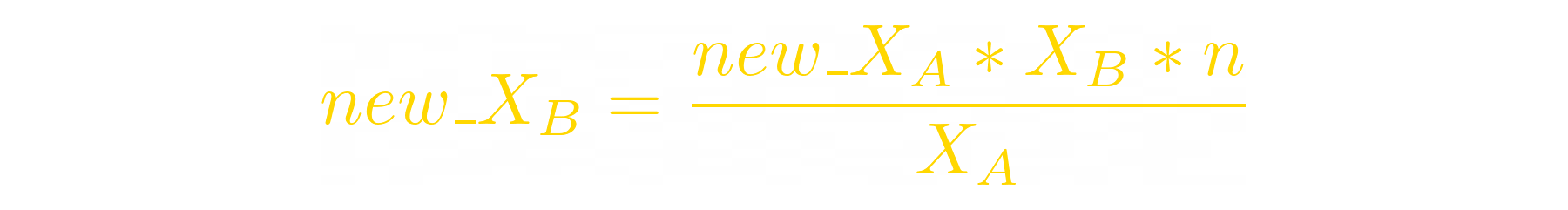
We can do this expression for all other tokens’ new balances:
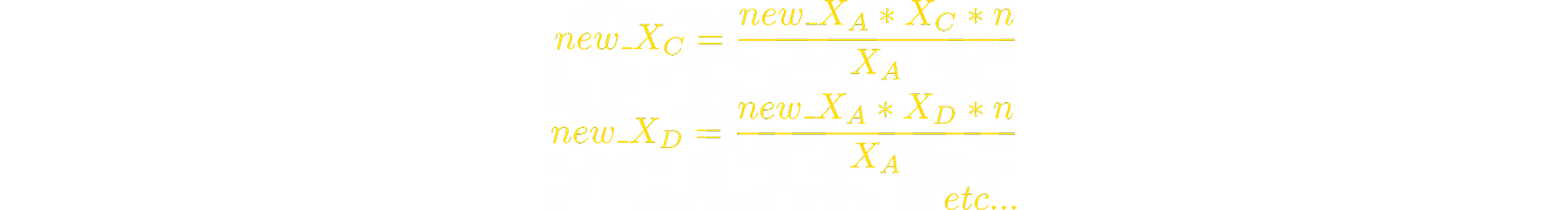
Let’s rewrite the invariant formula:
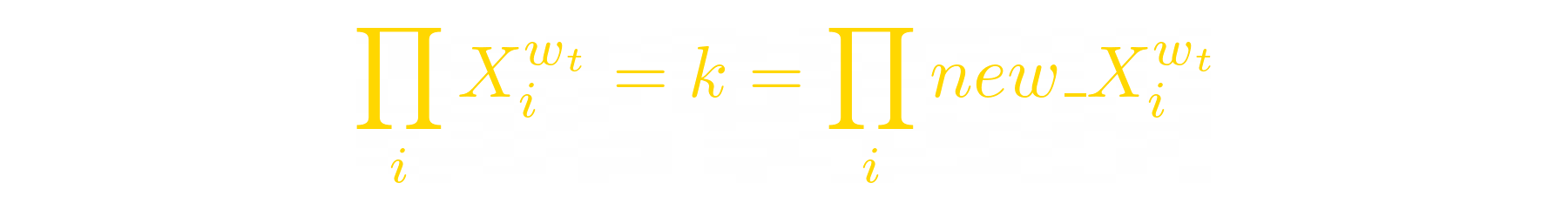
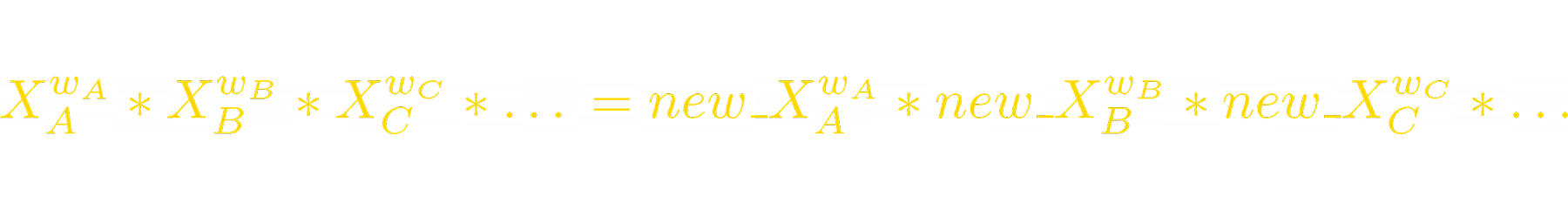
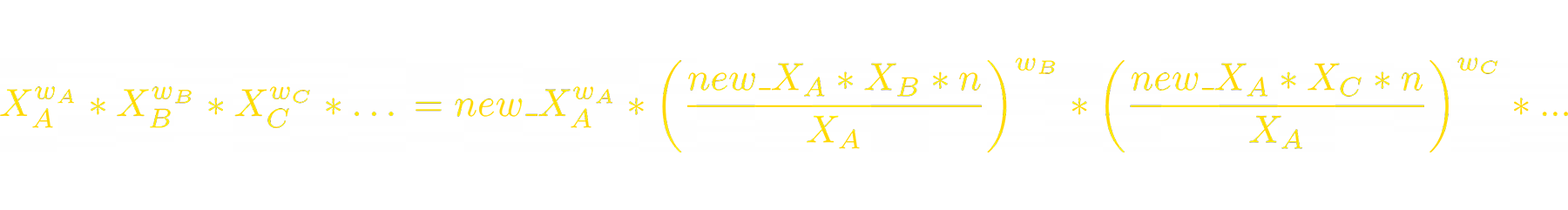
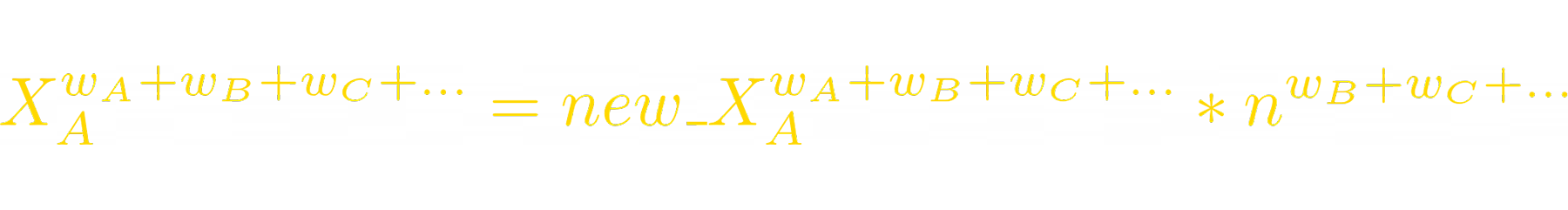
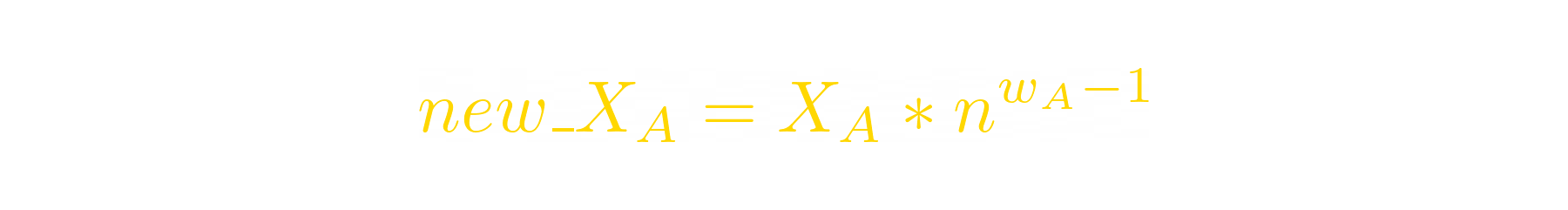
Now we can express the new balance of token_B:
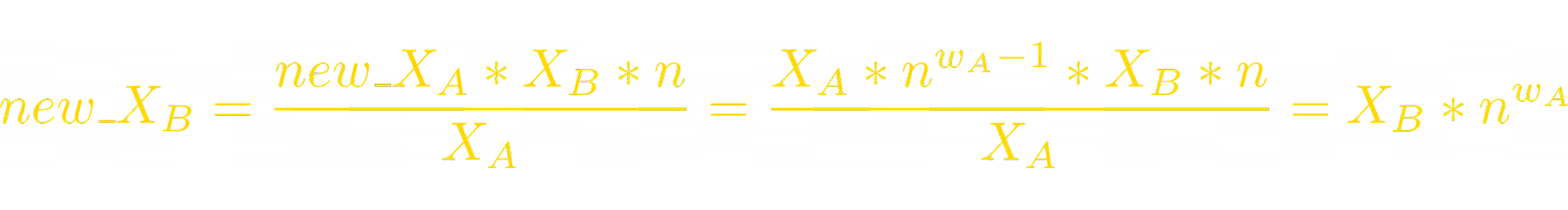
We can do this to all other tokens. So, to sum up, when A‘s price pumps n times, balances of tokens in the LP change as follows:
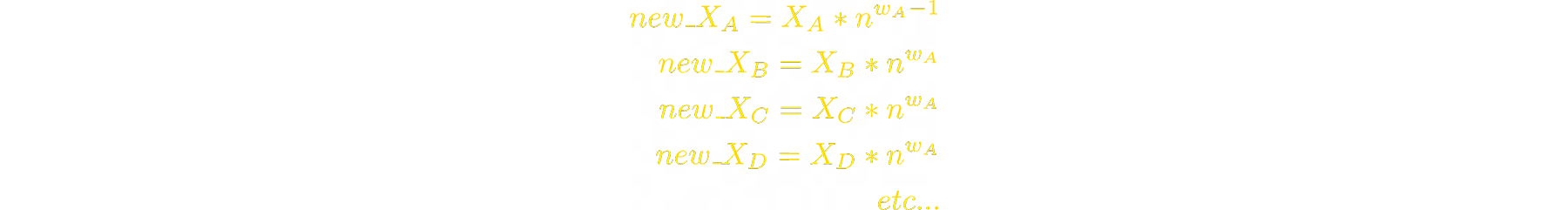
Now let’s calculate the Swap Fee Ratio for asymmetric LPs.
Let T is the amount of different tokens in the LP. Then each token’s weight in symmetric LPs is 1/T.
We need to consider the volatility of each token in the pool when calculating the average fees generated. Let each token’s price volatility be the same on average when compared to other tokens.
First we’ll need to calculate swap fees for symmetric LP.
When token i pumps n times, arbitrageurs sell all other tokens to the pool:
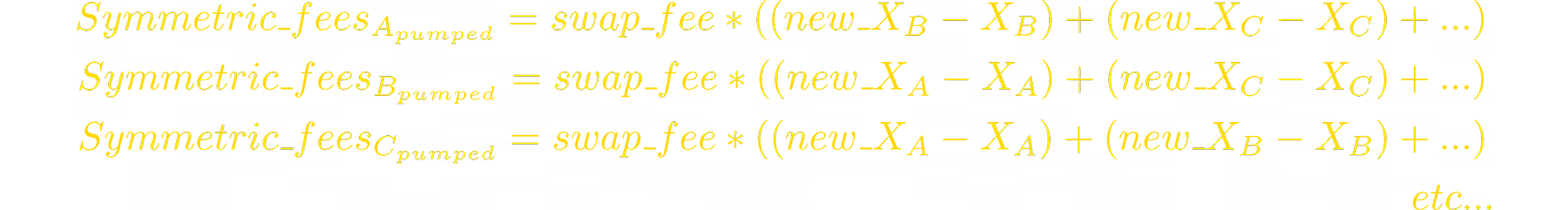
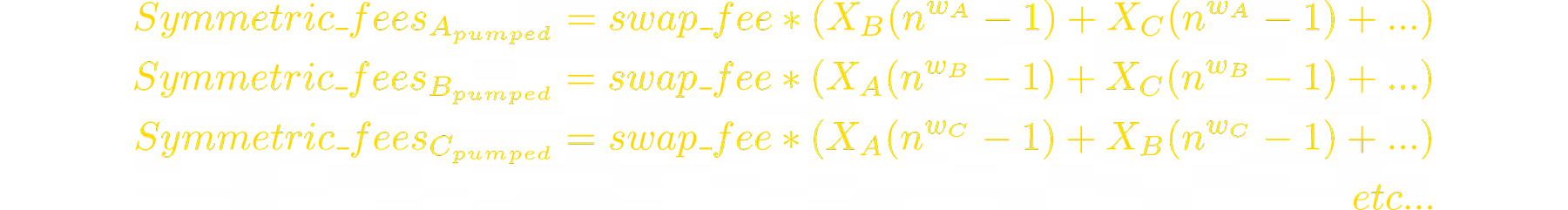
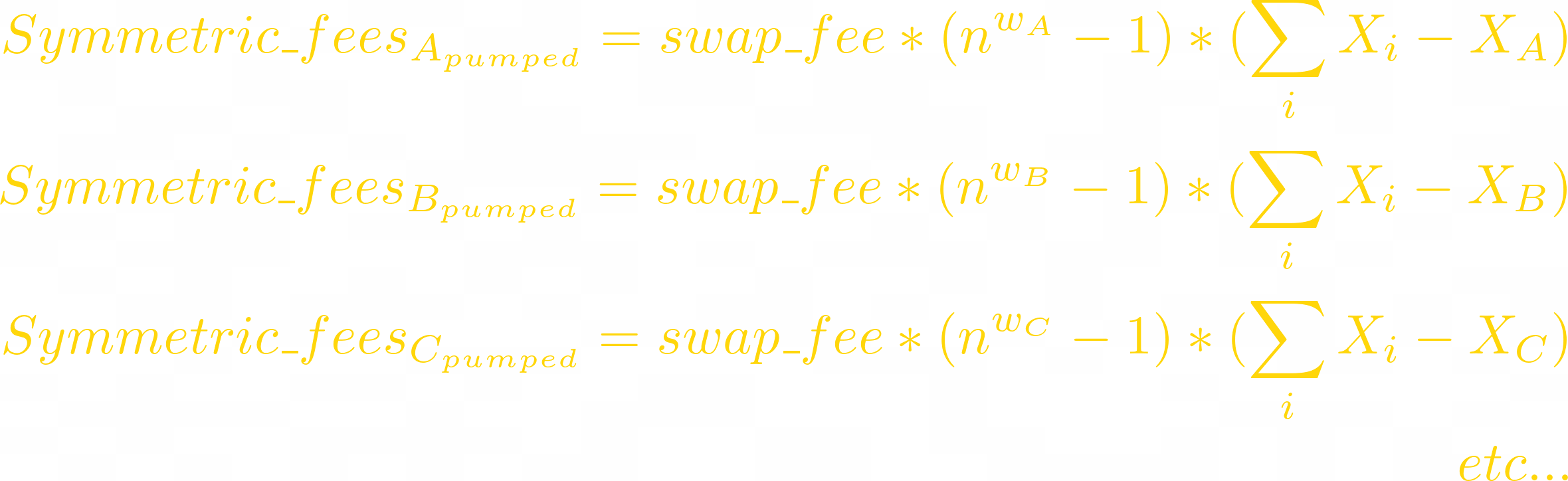
When token i dumps n times (pumps n^(-1) times), arbitrageurs sell it to the pool:
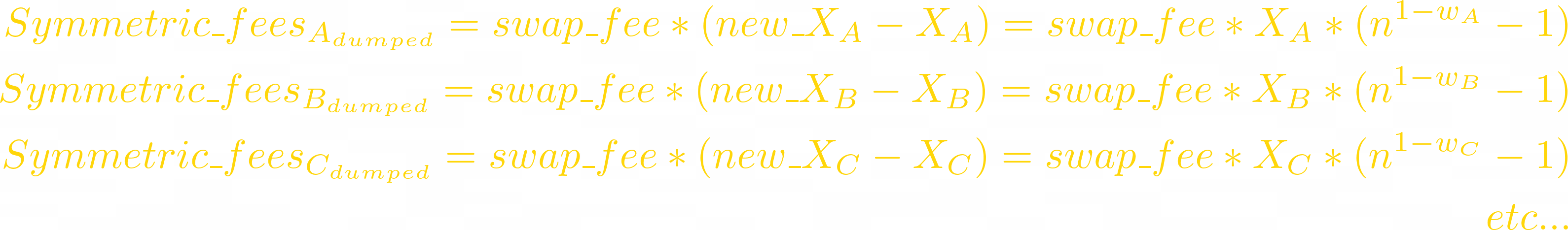
Since this LP is symmetric, let’s replace weights with 1/T:
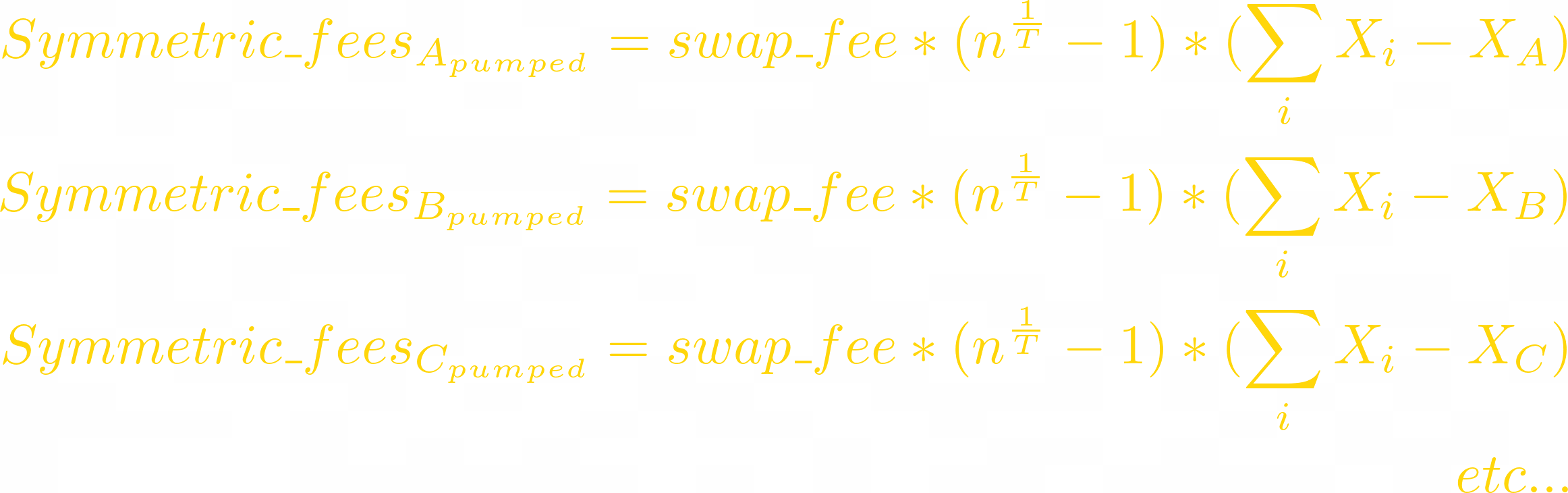
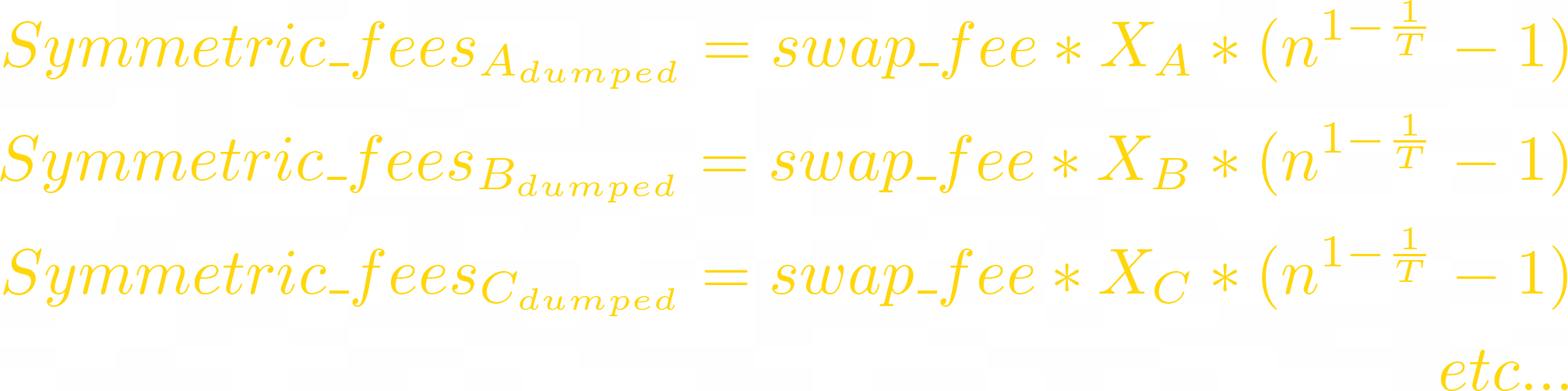
Now let’s calculate the same fees but for asymmetric LPs. Formulas are similar but the token amounts (Xᵢ) are different. To show asymmetry they must be calculated as:
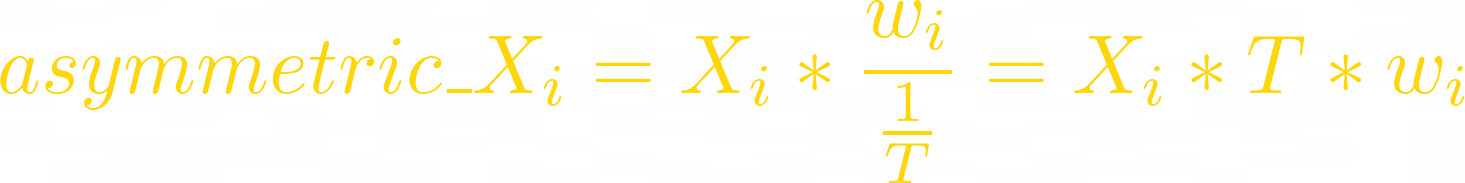
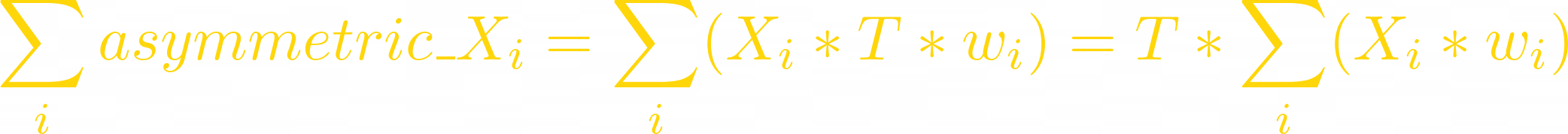
The swap fees generated on volatility in asymmetric LP are:
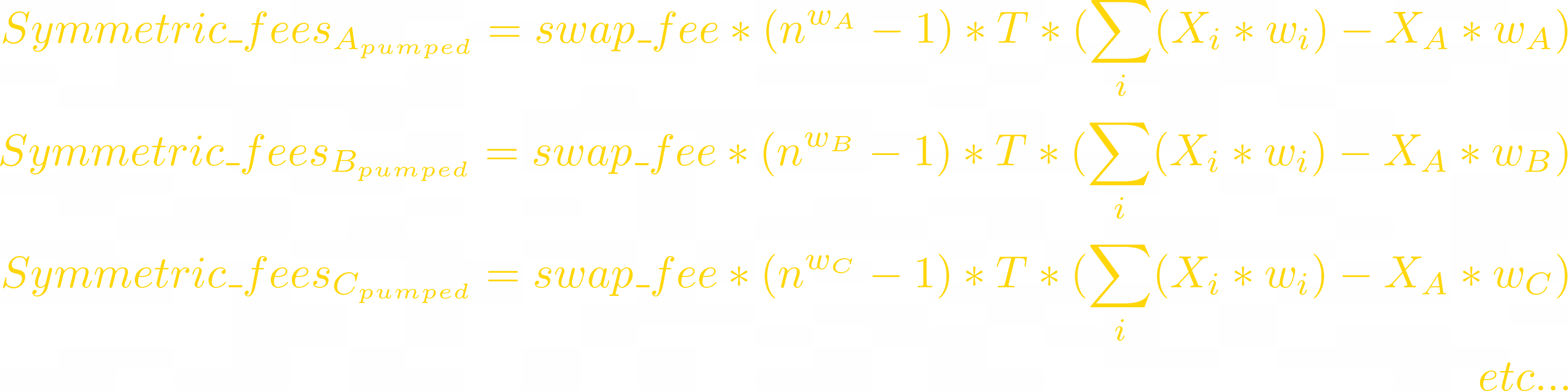
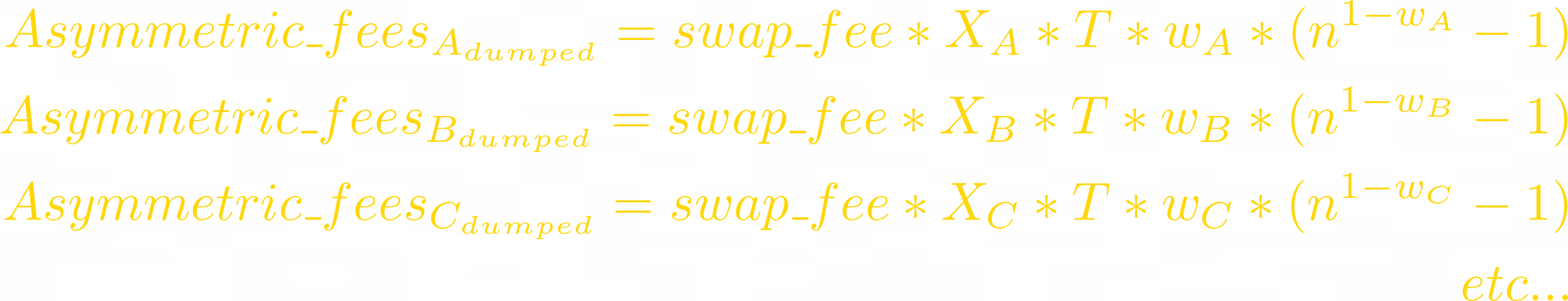
Now we can start calculating the Swap Fee Ratio:
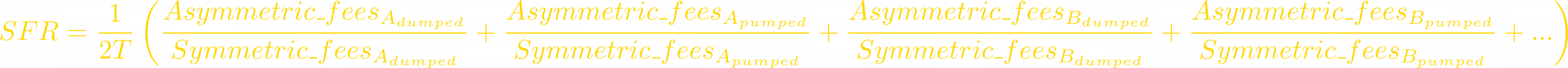
We’re trying to prove that SFR converges to a parabola when price change is small.
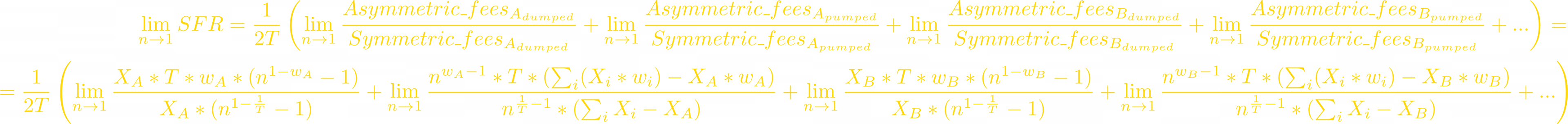
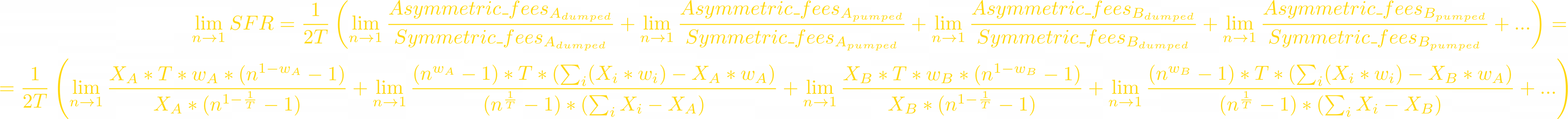
All numerators and denominators in these fractions equal to 0 when n=1, but we can use L'Hôpital's rule:
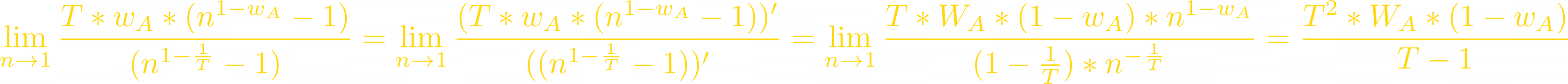
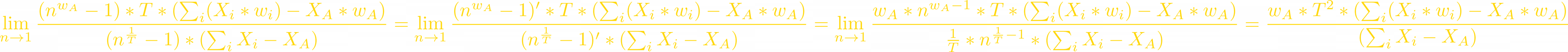
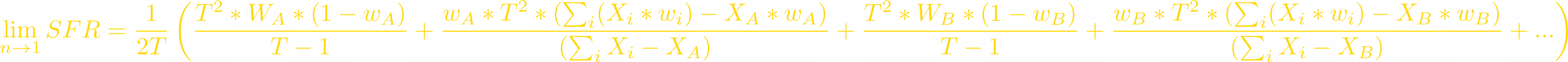
Since we consider all tokens’ volatility the same, what’s important to us is the relative price change and the relative change of individual token balance. We will set all Xᵢ to 1:
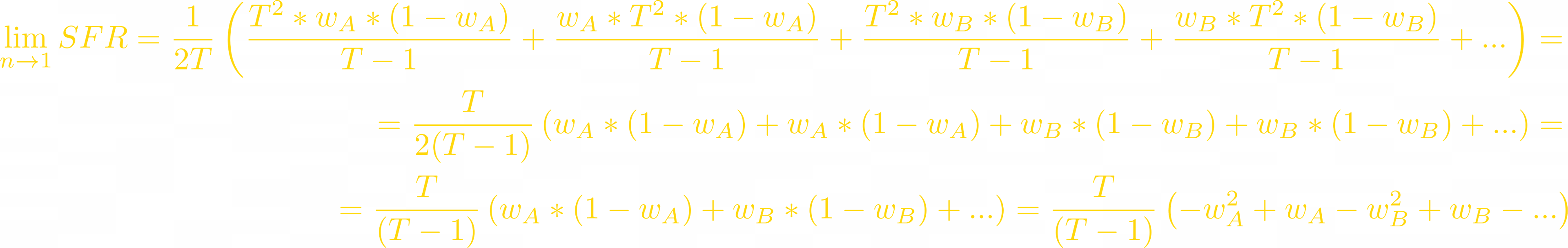
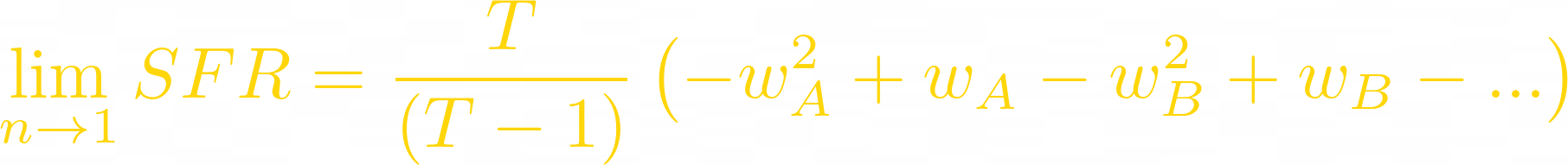
The SFT indeed converges to a quadratic function, just as we predicted.
When T = 2, it is a parabola as we saw before:
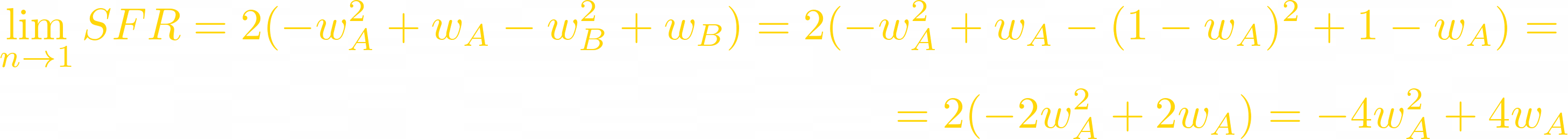
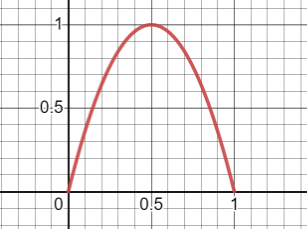
SFR is largest in symmetric LP — when each weight equals 0.5
And when T = 3, it is an elliptic paraboloid:
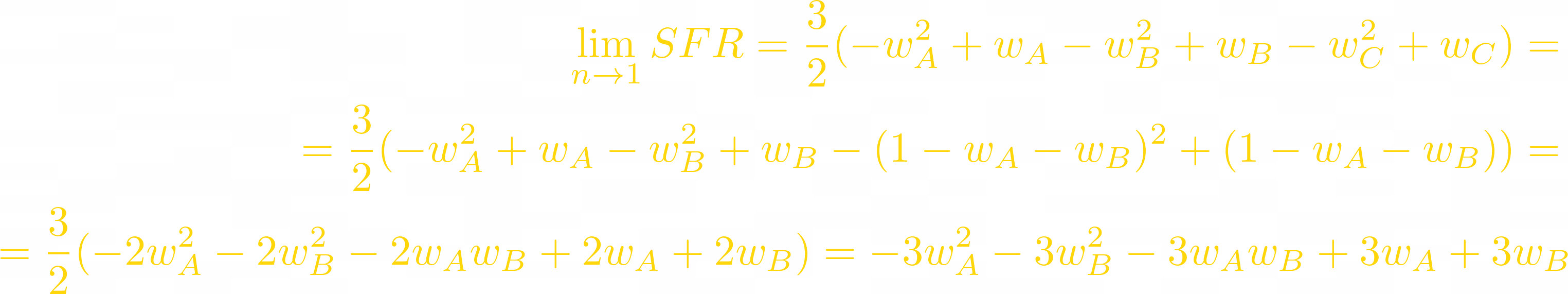
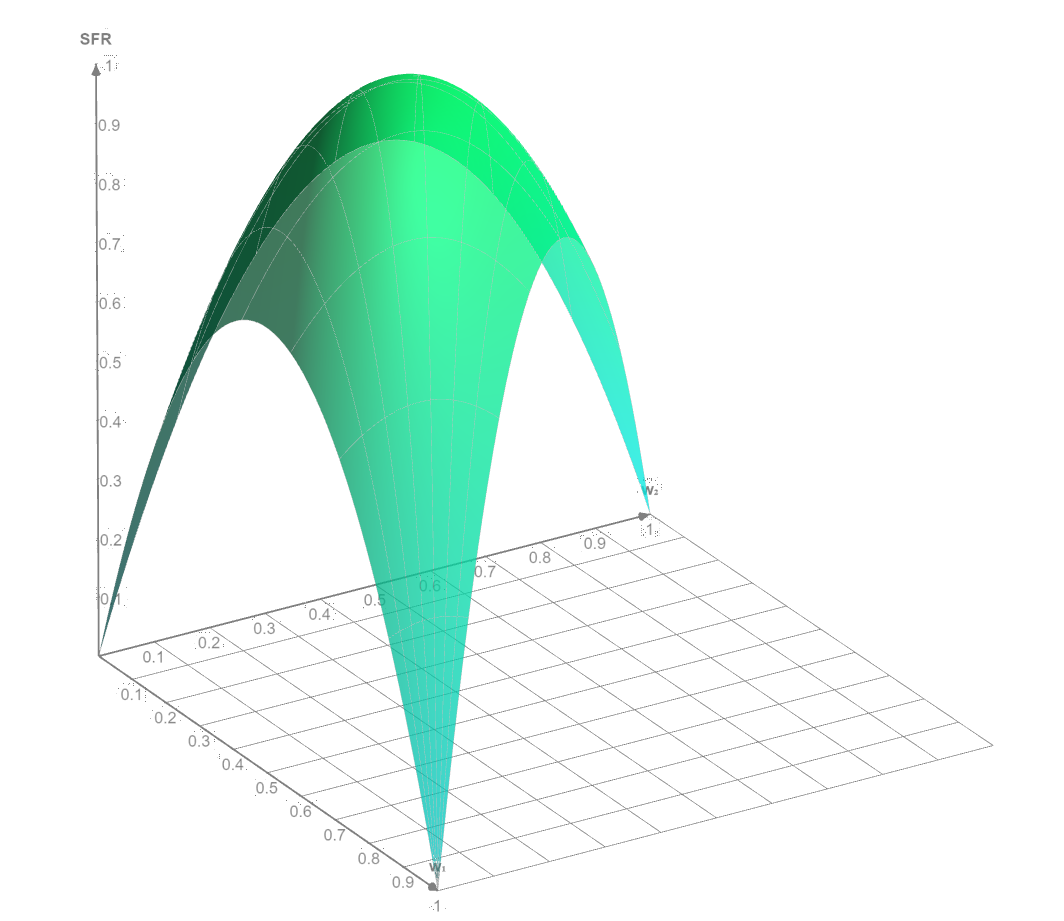
Here SFR is the largest and equals to 1 in a symmetric LP (each weight equals to 1/3)
P.S. Sorry for formulas as images, I transferred this post from mirror which didn't have LaTeX support.
